База знаний студента. Реферат, курсовая, контрольная, диплом на заказ
Архимед — Биографии
(около 287 — 212 до н. э.)
Архимед был одним из самых замечательных ученых Древней Греции. Наверное, вы слышали легенду о том, как был открыт один из законов физики.
Однажды, погрузившись в ванну в купальне, Архимед заметил, что своим телом он вытеснил часть воды и она выплеснулась, а при этом вода его как бы поддерживала. Ученый сразу понял, что здесь и заключается решение мучавшей его проблемы. С криком “Эврика!” (Нашел!”) он выскочил из купальни и помчался по улице: ему не терпелось сделать вычисления. Так был открыт знаменитый архимедов закон выталкивающей силы. Этот человек соорудил невиданные до той поры метательные военные машины для обороны города Сиракузы на острове Сицилия (где он родился и жил), которые сеяли панику и ужас в рядах римских легионеров и обращали их в бегство. Придумал он и способ поджигать вражеские корабли — с помощью тысячи больших зеркал, которые держали в руках воины осажденного города. Этими зеркалами солнечные зайчики были сфокусированы в единый луч, который и воспламенил суда неприятеля.
Параллелограмм сил или скоростей, о котором говорят на уроках физики, также изобретение Архимеда. Теория простых механизмов, разработанная великим ученым, привела к развитию важных разделов механики. Винт Архимеда применяется в различных машинах, служит для подъема сыпучих грузов, перемещает детали на заводах. Огромный (по тем временам) корабль “Сиракосия” был спущен на воду с помощью системы блоков, которой управлял один воин. Архимедово правило рычага и сейчас называют иногда золотым правилом механики. И именно ему легенда приписывает слова: “Дайте мне точку опоры, и я переверну мир!”
Несколько менее известно, что Архимед был не только замечательным механиком и физиком, но и гениальным математиком. Что же сделал он в этой области знания, какие его мысли и теории вошли сегодня в золотой фонд науки? Здесь прежде всего нужно сказать о вычислении длин. Известно, что длина окружности с радиусом R равна 2?R, где ? — некоторое число, несколько большее чем 3. Это видно из рассмотрения правильного вписанного шестиугольника: его периметр равен 6R, а длина окружности чуть больше! Как же поточнее вычислить значение ?? Именно Архимед в своем изящном исследовании, связанном с рассмотрением вписанных и описанных многоугольников, дал замечательную для своего времени оценку числа л. Он установил, что это число заключено между 3 10/71 и 3 1/7 . Вооружитесь микрокалькулятором, и вы легко обнаружите, что эти числа записываются в виде 3,140845 и 3,142857. Таким образом, Архимедом было найдено приближенное значение ? 3,14, которым мы и сейчас пользуемся для расчетов с не очень большой точностью.
Замечательно и другое открытие Архимеда, также связанное с измерением длин. Вам нужно по возможности точно измерить длину скамейки. Вы сначала определяете, сколько раз в скамейке откладывается метр; если имеется остаток — узнаете, сколько в нем дециметров; если снова есть остаток — находите, сколько в нем сантиметров, миллиметров. Такой процесс измерения был логически исследован Архимедом, который в связи с этим сформулировал аксиому, и сейчас называемую аксиомой Архимеда. Она состоит в том, что, взяв какой-либо отрезок (единицу измерения) и откладывая его на другом отрезке (каким бы большим он ни был), мы после некоторого числа откладываний обязательно дойдем до конца измеряемого отрезка и “перескочим” через его конец. Не правда ли, это настолько очевидно, что кажется, незачем и говорить об этом пустяке?! Но удивительное дело! Именно аксиома Архимеда сейчас особенно волнует умы ученых. Мы все чаще говорим теперь о “неархимедовой” геометрии, о “неархимедовых” системах чисел, о “неархимедовом” анализе. То, что Архимед сумел в седой древности вычленить и сформулировать именно такую аксиому, которая сегодня важна и актуальна, свидетельствует о большой его проницательности и научном предвидении. Еще одно открытие Архимеда связано с измерением площадей . Решая задачу, как построить отрезок, длина которого равна длине окружности данного круга, ученый вычислил отношение длины окружности к диаметру и нашел, что оно заключено 3 10/71 и 3 1/7. Созданный им метод вычисления длины окружности и площади фигуры, с помощью которого он получил результат, предвосхищает идеи особого интегрального исчисления, открытого (спустя два тысячелетия после Архимеда!) двумя другими гениями — И. Ньютоном и Г. В. Лейбницем. Именно Ньютон, который хорошо знал работы Архимеда и опирался на них, объяснял свои научные успехи тем, что “стоял на плечах гигантов”. Много важных открытий имеется в научном наследии Архимеда. Он установил теорему о том, что три медианы треугольника пересекаются в одной точке; нашел замечательные свойства кривой, которую теперь называют спиралью Архимеда; вычислил объем шара; создал формулу суммы убывающей геометрической прогрессии. Существует предание, что римский воинзавоеватель наступил ногой на чертежи, которые Архимед делал на влажном песке. “Не смей трогать мои чертежи!” — воскликнул ученый. Римскому воину было невдомек, что перед ним гений, слава которого переживет тысячелетия. Он пронзил ученого мечом. Обливаясь кровью, упал Архимед на свои чертежи, возможно заключавшие новое открытие.
Для подготовки данной работы были использованы материалы с сайта http://www.5.km.ru/
(около 287 — 212 до н. э.) Архимед был одним из самых замечательных ученых Древней Греции. Наверное, вы слышали легенду о том, как был открыт один из законов физики. Однажды, погрузившись в ванну в купальне, Архимед заметил, что своим тело
Реферат: Древнегреческий учённый-математик АРХИМЕД
| Название: Древнегреческий учённый-математик АРХИМЕД Раздел: Рефераты по математике Тип: реферат Добавлен 05:18:35 29 сентября 2005 Похожие работы Просмотров: 19030 Комментариев: 43 Оценило: 59 человек Средний балл: 4.4 Оценка: 4 Скачать | ||||||||||
| 13 октября 2019, 7:01 |
| Рубрика | Физика и энергетика |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 30.06.2014 |
| Размер файла | 32,1 K |

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru
Кубанский государственный университет
Реферат на тему: «Архимед как физик и математик»
Выполнила: студентка 1 курса
Архимед родился в 287 году до н.э. в Сиракузах на острове Сицилия. Отец Архимеда – астроном и математик Фидий. Фидий дал сыну хорошее образование. Затем Архимед продолжил своё обучение в Александрии, где познакомился со знаменитым астрономом Кононом, астрономом и математиком Эратосфеном, с которыми он поддерживал в дальнейшем научную переписку. Здесь он усиленно работал в богатейшей библиотеке, изучал труды Демокрита, Евдокса и других ученых. В те времена Александрия была культурным центром античного мира. Там был организован Мусейон, сообщество ученых, которые посвятили себя научным исследованиям и получали от царя плату за свои занятия. Они изучали четыре дисциплины – литературу, математику, астрономию и медицину. Ученые пользовались огромной по тому времени библиотекой, имевшей около 700000 книг.
После жизни в Александрии Архимед возвращается на родину в Сиракузы. Может быть, причиной уехать было то, что в Александрии царили лесть, заискивание, желание нравиться правителям Египта. А может быть в большей степени то, что Архимед не мог разделить модных в те времена воззрений на механику как на “ремесленный навык”, достойный раба. А ведь механика все более влекла его к себе. Но связи с Александрийской школой он не прерывал.
Большинство его работ написано в виде писем к его друзьям (Эраcтофену , Конону, Досифею). Домой, в Сиракузы, он привез богатый опыт научных исследований в различных областях: математика, физика, астрономия, продолжил заниматься и делать открытия в инженерном деле. В Сиракузах он живет без забот, он окружен почетом, вниманием и не нуждается в средствах. Впрочем, он мало думает о своем бытии, увлеченный вычислениями и изобретательством.
Легенды рассказывают, что Архимед забывал о пище, подолгу не бывал в бане и готов был чертить везде: в пыли, пепле, на песке, даже на собственном теле. Известно также, что Гераклид написал биографию Архимеда, не дошедшую до нас.
На 75-м году жизни был убит римским воином при взятии римлянами Сиракуз. Последние его слова, обращенные к своему убийце, содержали якобы просьбу не уничтожать чертеж, над которым он размышлял. Сто лет спустя Цицерон нашел могилу Архимеда по шару, вписанному в цилиндр, изображенному на могильном камне.
Об Архимеде – великом математике и механике – известно больше, чем о других ученых древности. Прежде всего достоверен год его смерти – год падения Сиракуз, когда ученый погиб от руки римского солдата. Впрочем, историки древности Полибий, Ливии, Плутарх мало рассказывали о его математических заслугах, от них до наших времен дошли сведения о чудесных изобретениях ученого, сделанных во время службы у царя Гиерона
Архимед — автор ряда необыкновенно глубоких и оригинальных работ по математике и физике этим отличается от Эвклида, который стал известен скорее как систематик знаний, существовавших до него.
архимед гидростатика оптический
1. Достижения в физике
Свои оптические теории Архимед строил на основе аксиом. Одной из таких аксиом являлась обратимость хода луча – глаз и объект наблюдения можно поменять местами. Весь же круг вопросов геометрической оптики -“катоптрики” был очень широк. Архимед занимался следующими проблемами: почему в плоских зеркалах предметы сохраняют свою натуральную величину, в выпуклых – уменьшаются, а в вогнутых – увеличиваются, почему левые части предметов видны справа и наоборот, когда изображение в зеркале исчезает и когда появляется, почему вогнутые зеркала, будучи поставлены против Солнца, зажигают поднесенный к ним трут, почему в небе видна радуга, почему иногда кажется, что на небе два одинаковых Солнца. С “катоптрикой” связана легенда о поджоге Архимедом римских кораблей во время осады Сиракуз.
Введение понятия центра тяжести.
Архимед первым ввел понятие центра тяжести в механике. Он заменяет тела их теоретическими моделями. Определение центра тяжести формулируется так: “. центром тяжести произвольного тела является некоторая точка, расположенная внутри него, обладающая тем свойством, что если за нее мысленно подвесить тяжелое тело, то оно останется в покое и сохранит первоначальное положение.” Понятие центра тяжести в дальнейшем было использовано Архимедом для установления законов рычага.
Открытие законов рычага.
Архимед вводит законы рычага на базе геометрии путем добавления к геометрическим аксиомам несколько “механических” аксиом:
1. Равные тяжести на равных длинах уравновешиваются, на неравных же длинах не уравновешиваются, но перевешивают тяжести на большей длине.
2. Если при равновесии тяжестей на каких-нибудь длинах к одной из тяжестей будет что-то прибавлено, то они не будут уравновешиваются, но перевесит та тяжесть, к которой будет прибавлено.
Архимед приводит аксиомы и на их основании доказывает теоремы. Наиболее важной является теорема об определении центра тяжести двух или нескольких фигур с помощью уравновешивания на рычаге (такое уравновешивание произойдет, если точка подвеса окажется в центре тяжести).
Закон рычага: рычаг находится в равновесии тогда, когда силы, действующие на него обратно пропорциональны плечам этих сил:
Архимед выводит законы гидростатики, используя физическую модель “идеальной жидкости”. Ученый установил, что:
1)”поверхность всякой жидкости, установившейся неподвижно, будет иметь форму шара, центр которого совпадает с центром Земли.”
2)”тела, равнотяжные с жидкостью, будучи опущены в эту жидкость, погружаются так, что никакая их часть не выступает над поверхностью жидкости и не будет двигаться вниз.”
3)”тело более легкое, чем жидкость, будучи опущено в эту жидкость, погружается настолько, чтобы объем жидкости, соответствующий погруженной части тела, имел вес, равный весу всего тела.”
4)”тела более легкие, чем жидкость, опущенные в эту жидкость, будут погружаться, пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела.” Открытие этой теоремы связывают с легендой о проверке плотности в короне.
Римский архитектор Витрувий, сообщая о поразивших его открытиях разных ученых, приводит следующую историю: “Во время своего царствования в Сиракузах Гиерон после благополучного окончания всех своих мероприятий дал обет пожертвовать в какой-то храм золотую корону бессмертным богам. Он условился с мастером о большой цене за работу и дал нужное ему по весу количество золота. В назначенный день мастер принес свою работу царю, который нашел ее отлично исполненной; после взвешивания корона оказалась соответствующей выданному весу золота. После этого был сделан донос, что из короны была взята часть золота и вместо него примешано такое же количество серебра.
Гиерон разгневался на то, что его провели, и не находя способа уличить это воровство, попросил Архимеда хорошенько подумать об этом. Тот, погруженный в думы по этому вопросу, как-то случайно пришел в баню и там, опустившись в ванну, заметил, что из нее вытекает такое же количество воды, каков объем его тела, погруженного в ванну. Выяснив себе ценность этого факта, он, не долго думая, выскочил с радостью из ванны, пошел домой голым и громким голосом сообщал всем, что он нашел то, что искал. Он бежал и кричал одно и то же по-гречески: “Эврика, эврика!” (“Нашел, нашел!)”. Затем, исходя из своего открытия, он, говорят, сделал два слитка, каждый такого же веса, какого была корона, один из золота, другой из серебра. Сделав это, он наполнил сосуд до самых краев и опустил в него серебряный слиток, и. соответственное ему количество воды вытекло. Так он нашел, какой вес серебра соответствует какому определенному объему воды. Затем он произвел такое же исследование для золотого слитка. Потом таким же методом был определен объем короны. Она вытеснила воды больше, чем золотой слиток и кража была доказана.
2. Достижения в математике
Во времена Архимеда ценили лишь «чистую» математику и презирали попытки применить математические знания на практике. Архимед шел как раз от практики, хотя в своих трудах большей частью маскировал свой интерес к прикладным исследованиям. Но именно поэтому его достижения настолько многогранны, что трудно представить, что они исходят от одного и того же человека.
Наступила эпоха нового времени, и его «низкий» подход был принят на вооружение. Это позволило достичь громадного прогресса во всех областях знания, которыми занимался Архимед. С уверенностью можно сказать, что он был бы очень горд, если бы знал о медали Филдса. Эта награда — своего рода Нобелевская премия по математике. В свое время Альфред Нобель не пожелал присуждать премию своего имени математикам, и потому канадец Джон Чарльз Филдс решил один раз в 4 года вручать награду человеку младше 40 лет за выдающиеся успехи в этой области знания. На этой престижной медали выгравировано изображение Архимеда. Тем самым он олицетворяет собой математику как таковую. Трудно более высоко оценить математический гений этого древнегреческого ученого. В наших учебниках математики и физики, во многих вещах и инструментах, которыми мы постоянно пользуемся, так или иначе отражен вклад Архимеда в историю человечества. Его достижения не ушли в прошлое. Они живут и в настоящем, освещая нам будничную жизнь.
Задача о трисекции угла.
Задача о делении угла на три равные части возникла из потребностей архитектуры и строительной техники. При составлении рабочих чертежей, разного рода украшений, многогранных колоннад, при строительстве, внутренней и внешней отделки храмов, надгробных памятников древние инженеры, художники встретились с необходимостью уметь делить окружность на три равные части, а это часто вызывало затруднения. Оригинальное и вместе с тем чрезвычайно простое решение задачи о трисекции угла дал Архимед.
Задача о квадратуре круга заключается в следующем: построить квадрат, площадь которого была бы равна площади данного круга. Большой вклад в решение этой задачи внес Архимед. В своем трактате “Измерение круга” он доказывает следующие три теоремы:
Теорема первая: Площадь круга равна площади прямоугольного треугольника, один из катетов которого равняется длине окружности круга, а другой радиусу круга.
Теорема вторая: Площадь круга относится к площади квадрата, построенного на диаметре, приблизительно, как 11:14.
Теорема третья: C-3d d, где С -длина окружности, а d-ее диаметр. Откуда, d



 Архимед родился в 287 году до нашей эры в греческом городе Сиракузы, расположенного на восточном побережье острова Сицилии, где и прожил почти всю свою жизнь. Отцом его был Фидий, придворный астроном правителя города Гиерона. Учился Архимед, как и многие другие древнегреческие ученые, в Александрии, где правители Египта Птолемеи собрали лучших греческих ученых и мыслителей, а также основали знаменитую, самую большую в мире библиотеку. После учебы в Александрии Архимед вновь вернулся в Сиракузы и унаследовал должность своего отца. В теоретическом отношении труд этого великого ученого был ослепляюще многогранным. Основные работы Архимеда касались различных практических приложений математики (геометрии), физики, гидростатики и механики.
Архимед родился в 287 году до нашей эры в греческом городе Сиракузы, расположенного на восточном побережье острова Сицилии, где и прожил почти всю свою жизнь. Отцом его был Фидий, придворный астроном правителя города Гиерона. Учился Архимед, как и многие другие древнегреческие ученые, в Александрии, где правители Египта Птолемеи собрали лучших греческих ученых и мыслителей, а также основали знаменитую, самую большую в мире библиотеку. После учебы в Александрии Архимед вновь вернулся в Сиракузы и унаследовал должность своего отца. В теоретическом отношении труд этого великого ученого был ослепляюще многогранным. Основные работы Архимеда касались различных практических приложений математики (геометрии), физики, гидростатики и механики. Машины Архимеда могли защитить город только от неприятельских приступов, но не могли спасти осажденных от голода. Марцеллу удалось, наконец, ворваться в город. Взятие Сиракуз, как и других городов, попавших в руки римлян, сопровождалось невероятными актами жестокости, убийствами и грабежами. В числе убитых был и Архимед.
Машины Архимеда могли защитить город только от неприятельских приступов, но не могли спасти осажденных от голода. Марцеллу удалось, наконец, ворваться в город. Взятие Сиракуз, как и других городов, попавших в руки римлян, сопровождалось невероятными актами жестокости, убийствами и грабежами. В числе убитых был и Архимед.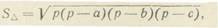 указанную формулу называют формулой Герона, потому что ему принадлежит заслуга широкого применения её на практике.
указанную формулу называют формулой Герона, потому что ему принадлежит заслуга широкого применения её на практике. носящий имя Архимеда), согласно которому на тело, погруженное в жидкость, действует сила, равная весу вытесненной им жидкости. Однажды приподнявши ногу в воде, Архимед констатировал с удивлением, что в воде нога стала легче. “Эврика! Нашел!” – воскликнул он, выходя из своей ванны. Анекдот занятный, но, переданный таким образом, он не точен. Знаменитое “Эврика!” было произнесено не в связи с открытием закона Архимеда, как это часто говорят, но по поводу закона удельного веса металлов – открытия, которое также принадлежит сиракузскому ученому и обстоятельные детали которого находим у Витрувия. Рассказывают, что однажды к Архимеду обратился Гиерон, правитель Сиракуз. Он приказал проверить, соответствует ли вес золотой короны весу отпущенного на нее золота. Для этого Архимед сделал два слитка: один из золота, другой из серебра, каждый такого же веса, что и корона. Затем поочередно положил их в сосуд с водой, отметил, на сколько поднялся ее уровень. Опустив в сосуд корону, Архимед установил, что ее объем превышает объем слитка. Так и была доказана недобросовестность мастера. Любопытен отзыв Цицерона, великого оратора древности, увидевшего “архимедову сферу” – модель, показывающую движение небесных светил вокруг Земли: “Этот сицилиец обладал гением, которого, казалось бы, человеческая природа не может достигнуть”. И, наконец, Архимед был не только великим ученым, он был, кроме того, человеком, страстно увлеченным механикой. Он проверяет и создает теорию пяти механизмов, известных в его время и именуемых “простые механизмы”. Это – рычаг (“Дайте мне точку опоры, – говорил Архимед, – и я сдвину Землю”), клин, блок, бесконечный винт и лебедка. Именно Архимеду часто приписывают изобретение бесконечного винта, но возможно, что он лишь усовершенствовал гидравлический винт, который служил египтянам при осушении болот.
носящий имя Архимеда), согласно которому на тело, погруженное в жидкость, действует сила, равная весу вытесненной им жидкости. Однажды приподнявши ногу в воде, Архимед констатировал с удивлением, что в воде нога стала легче. “Эврика! Нашел!” – воскликнул он, выходя из своей ванны. Анекдот занятный, но, переданный таким образом, он не точен. Знаменитое “Эврика!” было произнесено не в связи с открытием закона Архимеда, как это часто говорят, но по поводу закона удельного веса металлов – открытия, которое также принадлежит сиракузскому ученому и обстоятельные детали которого находим у Витрувия. Рассказывают, что однажды к Архимеду обратился Гиерон, правитель Сиракуз. Он приказал проверить, соответствует ли вес золотой короны весу отпущенного на нее золота. Для этого Архимед сделал два слитка: один из золота, другой из серебра, каждый такого же веса, что и корона. Затем поочередно положил их в сосуд с водой, отметил, на сколько поднялся ее уровень. Опустив в сосуд корону, Архимед установил, что ее объем превышает объем слитка. Так и была доказана недобросовестность мастера. Любопытен отзыв Цицерона, великого оратора древности, увидевшего “архимедову сферу” – модель, показывающую движение небесных светил вокруг Земли: “Этот сицилиец обладал гением, которого, казалось бы, человеческая природа не может достигнуть”. И, наконец, Архимед был не только великим ученым, он был, кроме того, человеком, страстно увлеченным механикой. Он проверяет и создает теорию пяти механизмов, известных в его время и именуемых “простые механизмы”. Это – рычаг (“Дайте мне точку опоры, – говорил Архимед, – и я сдвину Землю”), клин, блок, бесконечный винт и лебедка. Именно Архимеду часто приписывают изобретение бесконечного винта, но возможно, что он лишь усовершенствовал гидравлический винт, который служил египтянам при осушении болот.