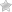Технологическая карта урока литературного чтения во 2 классе “С.Я. Маршак “Кот и лодыри”
Цель: познакомить со стихотворением С.Я. Маршака “Кот и лодыри”.
Задачи:
- Образовательные: познакомить с произведением С.Я. Маршака “Кот и лодыри”, с жизнью и творчеством С.Я. Маршака.
- Развивающие: развивать внимание, мышление, память, речь.
- Воспитательные: воспитывать любовь к чтению, уважительное отношение к одноклассникам, толерантность в групповых взаимодействиях, ответственное отношение к результатам своего учебного труда.
Средства обучения: учебник “Литературное чтение 2 класс”, Климанова Л.Ф., Горецкий Г.В., компьютер, презентация.
Ход урока
Деятельность учителя
Деятельность обучающихся
Мотивация к учебной деятельности
– Начать, сегодняшний урок я хотела бы с пословицы, которую вы видите на слайде: «Учиться всегда пригодится».
– Как вы понимаете значение этой пословицы?
– Я желаю вам, чтобы знания, полученные на уроке, пригодились вам.
Размышляют над пословицей.
– Учиться нужно на протяжении всей жизни.
Актуализация знаний
Речевая разминка.
– Сейчас давайте прочитаем скороговорку вместе, громко и четко.
– А теперь быстрее! И еще быстрее, без моей помощи, но также дружно!
– Кто может произнести скороговорку с вопросительной интонацией? А кто с восклицанием, восхищением? Давайте попробуем произнести ее, постепенно понижая голос. Кто желает попробовать? А теперь наоборот, постепенно повышая голос.
– Ребята, о ком говорится в скороговорке?
Проверка домашнего задания.
– С каким произведением вы познакомились на прошлом уроке?
– Кто были помощники Федоры?
– К сегодняшнему уроку вы учили наизусть отрывок из сказки «Федорино горе» о том, как коты помогали Федоре вернуть посуду, а так же нарисовали своих домашних котов.
Чтение отрывков наизусть.
– Посмотрите на выставку ваших рисунков.
– У вас у многих есть коты. Как зовут ваших питомцев? Как они выглядят и что любят делать? Расскажите. (1-2 человека)
– Ребята, я думаю вы уже догадались, кто же будет героем произведения, с которым мы познакомимся сегодня на уроке?
– Именно кот будет одним из главных героев нашего урока.
– Но в отличии от ваших котов, наш кот не такой красивый, он ободранный, но он хочет учиться, хочет стать умным, грамотным. Кроме кота есть и другие участники. Определите название стихотворения, с которым мы познакомимся сегодня на уроке. Оно зашифровано в записи на экране.
– Кто может уже ответить с каким произведением мы познакомимся сегодня?
– Откройте учебник на странице 24 учебника, прочитайте фамилию имя отчество автора стихотворения «Кот и лодыри».
– Тема, сегодняшнего урока: Стихотворение Самуила Яковлевича Маршака «Кот и лодыри».
– С чем познакомимся сегодня на уроке?
– Чему будем учиться?
Выполняют речевую разминку. Читают с разной скоростью и интонацией.
Отвечают на вопросы учителя.
– О кошке и мышке.
– Со сказкой К.И. Чуковского «Федорино горе».
Читают отрывок из сказки наизусть.
Рассказывают о домашних питомцах.
Определяют название произведения.
– Познакомится с стихотворением С.Я. Маршака «Кот и лодыри».
– Узнаем о жизни писателя.
– Будем учиться выразительному чтению стихотворение.
– Отвечать на вопросы по стихотворению.
Проблемное объяснение и фиксирование нового знания
Знакомство с автором
– Откройте учебник с 24 и прочитайте сведения об С.Я. Маршаке.
– Для кого писал С.Я.Маршак?
– Как вы понимаете: “Детские стихи Маршака настоящие?”
– Я теперь я вам подробнее расскажу о писателе
Рассказ с использованием презентации.
Родился 22 октября в Воронеже в семье талантливого изобретателя, мастера-мыловара. Раннее детство и школьные годы провел в городке Острогожске под Воронежем. В гимназии учитель словесности привил любовь к классической поэзии, поощрял первые литературные опыты будущего поэта. В 15 лет он переехал в Петербург, учился в одной из лучших гимназий, целые дни проводил в публичной библиотеке. Печататься начал в 20 лет. Позже для завершения образования Маршак уехал учиться в Англию. Два года он слушал лекции на факультете искусства Лондонского университета. Во время каникул много путешествовал пешком по Англии, слушал английские народные песни. Уже тогда начал работать над переводами английских произведений, впоследствии прославившими его. Затем в русских журналах были опубликованы первые переводы Маршака из английской поэзии. В 1914 вернулся на родину, публиковал свои переводы в журналах “Северные записки” и “Русская мысль”. В годы войны Маршак занимался помощью детям беженцев. В 33 года он жил в Краснодаре, организовал здесь один из первых в стране театров для детей, писал для него пьесы-сказки. Здесь началось творчество детского писателя. А еще через три года вышли первые стихотворные книжки для самых маленьких: “Дом, который построил Джек”, “Детки в клетке”, “Сказка о глупом мышонке”. Большую известность принесли Маршаку и его пьесы-сказки: «Кошкин дом», «Двенадцать месяцев» и др. Стихи самого Маршака переведены на многие языки народов мира. В 77 лет, 1964 года, писатель ушел из жизни.

– Вот такая интересная жизнь была у С. Я. Маршака.
Знакомство с стихотворение
– А теперь давайте перейдем к нашему стихотворению. Откройте стр. 26.
– Как вы думаете, о чем будет говориться в произведении с таким название? Посмотрите на иллюстрацию, может она вам подскажет.
– Будут ли кот и лодыри приятелями, друзьями? Что у них может случиться? Интересно вам стало узнать, о чем оно?
– Давайте проверим наше предположение.
– Сейчас я включу запись, ваша задача внимательно слушать и следить по тексту.
– Итак, вот мы и послушали. Какие непонятные слова вам встретились? Давайте их разберем.
Словарная работа.
Лодыри – бездельники, лентяи.
Грифель – пишущий стержень внутри карандаша.
– Понравилось вам стихотворение?
– Какое настроение оно вызывает?
– О чем рассказывается в стихотворении?
– Кто главные герои?
Работают с учебником. Читают статью об авторе. Отвечают на вопросы.
– Для взрослых и детей.
– Они доставляют радость и взрослым и детям.
Воспринимают на слух биографию писателя.
Делают предположения.
Воспринимают на слух художественный текст. Объясняют лексическое значение слов.
Определяют смысл произведения. Отвечают на вопросы.
-О том, что ребята, которые не очень любят учиться, вместо того, чтобы пойти на урок, отправились кататься на коньках.
– Кот, лодыри, автор.
Физ. минутка
Первичное закрепление во внешней речи
Чтение и анализ стихотворения.
– А сейчас давайте прочитаем стихотворение вместе по цепочке. По ходу чтения будем отмечать слова и наших героев карандашом.
– Куда попали лодыри по пути на урок?
– Найдите в тексте описание кота
– На что жаловался кот? Найдите. Прочитайте
– Почему кот хочет научиться грамоте? Найдите и прочитайте
– Лодырям нравится учиться?
– Чем занимаются лодыри целый день?
– Разве это плохо кататься на коньках, заниматься спортом, дышать свежим воздухом?
– Когда можно играть, кататься на санках, лыжах, коньках?
– В этом стихотворении автор на чьей стороне: кота или лодырей?
– Как Маршак относится к мальчишкам-лодырям?
– Каких людей он высмеивает?
– В каких строчках заключена главная мысль стихотворения?
– Как вы думаете, какие же качества характера помогают добиться успехов в учёбе и в жизни?
– Какой же урок можно вынести из стихотворения С.Я. Маршака?
Работа в паре
– Выберите слова, которые характеризуют кота:
умный, мудрый, заботливый, ворчливый, ученный, грамотный, надоедливый.
– Найдите в тексте слова, которые говорит кот. Прочитайте друг другу, обсудите.
– Найдите слова, близкие по значению к слову лодырь:
бездельник, лентяй, лежебока, неряха, грязнуля.
– Найдите в тексте слова лодырей, прочитайте друг другу, обсудите.
Читают стихотворение. Рассказывают о героях, отражая собственное отношение к ним.
– На то, что он не может учиться.
– Потому то без грамоты пропадешь.
– Катаются на коньках.
– Нет, всему должно быть своё время.
– Он смеется над ними, осуждает их.
– Без грамоты пропадёшь, далеко без грамоты не уйдешь.
– Не лениться, чтобы не произошла беда, бороться со своей ленью, воспитывать в себе силу воли.
Работают в паре.
Отвечают на вопросы.
Самостоятельная работа с самопроверкой
Работа в группах
– Сейчас вам предстоит в группах подготовить выразительное чтение по ролям стихотворения.
Выразительное чтение по ролям.
– Чьё чтение вам понравилось больше всего?
Читают текст в группах. Организовывают взаимоконтроль. Оценивают свое чтение.
Включение в систему знаний и повторение
– С каким стихотворением вы познакомились на уроке?
– Кто автор стихотворения «Кот и лодыри» ?
– Что узнали о писателе?
– Чему учит стихотворение?
– Прочитайте пословицы на экране и соотнесите смысл пословиц с содержанием стихотворения.
Учись с молоду – пригодится в старости.
Мудрым никто не родился, а научился.
Лентяй не дела ищет, а от дела рыщет.
У лодыря что ни день, то лень.
Отвечают на вопросы. Обобщают изученный материал. Соотносят смысл пословицы с содержанием произведения.
– Самуил Яковлевич Маршак.
Рефлексия учебной деятельности на уроке
– Наш урок подходит к концу продолжите предложения на экране Сегодня на уроке:
Знания полученные на уроке…
1. выразительное чтение по ролям;
2. чтение наизусть отрывка стихотворения;
3. составить совет лодырям «Почему нельзя пропускать уроки?»
Отвечают на вопросы. Осуществляют рефлексию.
Маршак «Кот и лодыри». Кто главные герои и какая главная мысль?
Маршак «Кот и лодыри» кто главные герои?
Маршак «Кот и лодыри» главная мысль произведения какая?
Маршак «Кот и лодыри» характеристика главных героев.
![]()
Главные герои, соответственно, кот и лодыри.
Кот мечтает учится, но “школы не построены для котят, научить нас, лодыри, не хотят”. А лодыри прогуливают уроки, катаясь на катке.
Главной мыслью произведения я бы выделил следующую “. а теперь без грамоты пропадёшь, далеко без грамоты не уйдёшь”.
Писал по памяти, так что могут быть неточности в цитатах.
Характеристика лодырей: нет желания учится, предпочитают учёбе физическое развитие.
Характеристика кота: усатый, молодой (скоро год), может разговаривать с людьми, мечтает учиться читать и писать, считает себя умным и красивым.
![]()
Ответ на вопрос викторины: американский мультипликатор УОЛТ ДИСНЕЙ. (но не он снял мультфильм по пьесе Маршака “12 месяцев”, а русский режиссёр Иванов-Вано)
История с пьесой Самуила Маршака “12 месяцев”, о которой во время войны Уолт Дисней писал письмо, которое затерялось, а потом нашлось, теперь известна всем.
Но есть ещё интересные подробности о том, что первый фестиваль Уолтовской мультипликации прошёл в Москве ещё в 1933 году.
Иосиф Сталин стал большим поклонником творчества Диснея, ему очень понравился Микки-Маус, например.
Высоко оценил Уолта Диснея и Эйзенштейн. Вот что он писал о создателе “империи мультипликации” Уолте Диснее:
Известно, что они переписывались и в музее Эйзенштейна в Москве хранится автограф, присланный Уолтом Диснеем.
Поэтому, мне кажется, что если бы письмо пришло вовремя и в той манере, того времени был сделан мультфильм по пьесе С. Маршака “12 месяцев”, то он был бы таким же милым как и наш советский, снятый в 1956 году режиссёром Ивановым-Вано.
В то время образы были менее урбанистичными, на мой взгляд.
![]()
Напишем правильные ответы на вопросы теста по сказке “Двенадцать месяцев” Маршака:
Произведение, которое пишется, чтобы его поставили на подмостках сцены, называется пьеса. Ответ – б.
Персонажей в произведении Маршака много, но главными являются Королева и девочка. Ответ – в.
Королева хотела, чтобы у нее были цветы, которые растут весной, а не зимой. Ответ – в.
Королева делала много разных глупостей, но большой промах она совершила, когда без раздумий решила судьбу постороннего человека. Ответ – в.
Девочка отправилась в лес по велению мачехи. Ответ – б.
На дворе был декабрь, именно этот месяц уступал свои права следующему брату. Ответ – в.
Герои ответили добром на добро. Девочка всегда с уважением и бережностью относилась ко всему в лесу. Ответ – б.
Волшебный предмет оказался у главной героини от четвёртого месяца. Ответ – б.
Когда девочка оказалась в лесу у месяцев, то она показала себя невоспитанной, жадной гостьей. Ответ – б.
В конце сказки отрицательные героини в наказание за свои поступки стали собачками. Ответ – а.
Изменения возможны только в том случае, если рядом есть положительный пример, который научит чуткости, доброте, верности.
Ему Королева приказала вырубить самую прекрасную ёлочку, чтобы удивить гостей.
Ее отправили за хворостом и дровами.
Исходя из описания всех 12 месяцев, трое из них были старики – это зимние месяцы, а трое – совсем мальчишки – это весенние месяцы. Получается по календарному году, что самый старший – февраль, самый младший – март.
Уроки доброты, вежливости, верности, сострадания, ценности знания.
Потому что девочка понимает, что перед ней избалованный ребёнок. Ей некому было на своем примере показать что такое милосердие, любовь, чуткость. Королева была лишена этого, ведь вокруг нее находились только слуги, которые выполняли любую ее прихоть.
Потому что она является воплощением добра, сердочности, понимания. А в сказках добро всегда побеждает зло.
Сказка названа так, потому что именно эти персонажи помогли девочке исполнить задание. Через взаимодействие с ними видны характеры и поступки всех героев.

![]()
В сказке Самуила Яковлевича Маршака ” Сказка о глупом мышонке” много нянек приглашала к сыночку мама-мышка. Но никто ему не нравился, как поет. Была, утка, была жаба, лошадь и курица. Пригласили рыбку щуку в няньки. Но и она не понравилась глупому мышонке. Но щука не пела, не баюкала малыша, а только разевала рот. И опять не понравилась нянька мышонку. И,наконец, позвала мама кошку. И так уютно мурлыкала кошка, что малыш стал засыпать. А кошка- то его и съела.
Вот такой грустный конец у сказки.
![]()
В забавном стихотворении Самуила Маршака “Вот какой рассеянный” читатель знакомится с очень невнимательным человеком. Из-за своей рассеянности он попадает в нелепые ситуации. Он не может нормально одеться, так как путает одежду, даже вместо шапки он надевает сковороду. Не может рассеянный поговорить с вагоновожатым, так как путает даже слова. По ошибке он садится в отцепленный вагон и никуда не уезжает из города, хотя сидит в вагоне двое суток.
Нарисовать рисунки к стихотворению не так просто. Конечно хочется нарисовать главного героя, а рисовать человека сложно. Но рисунок рисуют дети, поэтому усложнять не стоит, а человека можно нарисовать по схеме.

Можно попробовать нарисовать мужчину как на этом детском рисунке.
Для этого нужно для начала обозначить высоту человека. Рисовать лучше с головы, ее рисуем в форме овала простым карандашом. Далее туловище, руки и ноги. Можно нарисовать мужчину в пальто, о котором говорится в стихотворении, можно просто в костюме. На голове у бедолаги рисуем сковородку, которую он схватил вместо шапки, а на ногах можно нарисовать перчатки, ведь именно их герой стихотворения натянул вместо валенок.
Нарисовать фигуру мужчины можно примерно по такой схеме:
Вот еще пример детского рисунка по стихотворению “Вот какой рассеянный”:

На этом рисунке рассеянный изображен у себя дома, где он вместо шапки надевает сковороду, а вместо обуви перчатки.
Можно также нарисовать мужчину в трамвае, на вокзале или в вагоне, в который он сел по ошибке.
Можно нарисовать ситуацию, как герой надевает брюки вместо рубашки. Можно, например, срисовывать с подобного рисунка:

Нарисовать мужчину, сидящего на кровати. Руки он просовывает в штанины, так как вместо рубашки надевает брюки.
Стихотворение С. Я. Маршака «Кот и лодыри» для читательского дневника
Произведение С. Я. Маршака «Кот и лодыри» было написано в 1933 году. Это интересное и поучительное стихотворение. Автор рассказывает про встречу бездельников и уличного кота. На примере героев автор показал, что очень важно не лентяйничать, а учиться и стремиться к знаниям, всегда быть при деле. Краткое содержание «Кот и лодыри» для читательского дневника поможет понять смысл стихотворения и замысел автора.
- Анализ произведения
- Краткое содержание
- План пересказа
- Описание героев и главная мысль
- Отзывы читателей
Анализ произведения
Сюжет развивается зимой. В стихотворении показана важность знаний в жизни людей.
Краткое содержание
Школьники решили прогулять уроки и пошли на каток. По дороге им встретился кот. Он был очень хмурым, серьезным, подранным и несчастным.
Ребята спросили у него, отчего тот так печален.
Кот поведал им о своих горестях. Он был умным, но безграмотным. Печалился, что для котят не строят школ, а ведь сейчас без грамоты никуда. Нельзя добыть пропитание, питье, да и номер дома не прочитать. Поэтому всем животным очень плохо живется необразованными.
Мальчишки весело сообщили, что им уже скоро 12, а они толком ничего не знают. Им лень учиться, да и знания не нужны. Ведь это скучно, а вот катание на катке — другое дело, гораздо лучше книги.
Кот был удивлен такими словами. Он много повидал таких бездельников на своем пути, но таких глупцов — ни разу.
План пересказа
По краткому содержанию можно составить сжатый план стихотворения. Он состоит из следующих пунктов:

- Мальчишки прогуляли школу.
- Дорога на каток.
- Встреча с умным котом, его рассказ про печали и переживания.
- Школы для котят.
- Жизнь необразованных котов.
- Ребята признались, что ничего не знают, а школу считают скучной.
- Удивление кота.
Описание героев и главная мысль
В стихотворении представлено несколько главных героев:
- Лодыри — ленивые и безответственные мальчишки. Они не желают учиться, считают, что лучше веселиться на катке, чем ходить на скучные уроки.
- Кот — уличный, но любознательный. Он хочет обучиться грамоте, мечтает о создании школ для котят.

Основная мысль произведения заключается в том, что знания — это великая сила. Необразованному человеку сложно устроить свою жизнь, прожить ее полноценно.
Жизненная цель людей — постоянно учиться, развивать свои навыки, передавать свой опыт.
Стихотворение учит следующему:
- любить и ценить знания;
- уважить педагогов;
- быть трудолюбивым и настойчивым;
- достигать своих целей.
Знания делают жизнь лучше и интереснее. Поэтому к ним нужно стремиться, ходить в школу и прилежно учиться.
Отзывы читателей
Очень интересное стихотворение. В нем затронута важная тема, а именно грамотность, желание учиться. Я считаю, как человек относится к повседневной жизни, так она и сложится. Если нет желания учиться, то потом и работать не захочется. Человек всю жизнь будет лениться, так и проживет, ожидая пенсии, когда можно будет ничего не делать. Каждый день определяет все дальнейшее существование. Маршак (кто написал «Кот и лодыри») — автор очень талантливый. Он говорит о сложных вещах простым языком, что позволяет детям осознать их. Я очень советую обязательно каждому прочитать все его стихотворения.
Все произведения автора очень интересны. Помимо этого, мне еще нравится у Маршака «Почта», краткое содержание для читательского дневника которого составляли в классе совсем недавно, а еще делали рисунок по нему. Рекомендую прочитать сборник стихов, поучительно и увлекательно.
В школе нам задавали сделать анализ «Кот и лодыри», написать по стихотворению конспект. Мне книга очень понравилась, особенно если читать с картинками. Сразу представляешь, как выглядят герои: умный, но подранный котик, мальчишки-бездельники. Это интересное и поучительное произведение. «Кот и лодыри» написал С. Я. Маршак. У автора много разных стихов, во всех можно чему-нибудь научиться. Особенно мне нравятся стихотворения про животных. Автор передает читателям свое теплое отношение к ним, как бы наставляет нас на такое же поведение. Советую.
Теорема Виета
После того, как вы внимательно изучите, как решать квадратные уравнения обычным образом с помощью формулы для корней можно рассмотреть другой способ решения квадратных уравнений — с помощью теоремы Виета.
Перед тем, как изучить теорему Виета, хорошо потренируйтесь в определении коэффициентов « a », « b » и « с » в квадратных уравнениях. Без этого вам будет трудно применить теорему Виета.
Когда можно применить теорему Виета
Не ко всем квадратным уравнениям имеет смысл использовать эту теорему. Применять теорему Виета имеет смысл только к приведённым квадратным уравнениям.
Приведенное квадратное уравнение — это уравнение, в котором старший коэффициент « a = 1 ». В общем виде приведенное квадратное уравнение выглядит следующим образом:
Обратите внимание, что разница с обычным общим видом квадратного уравнения « ax 2 + bx + c = 0 » в том, что в приведённом уравнении « x 2 + px + q = 0 » коэффициент « а = 1 ».
Если сравнить приведенное квадратное уравнение « x 2 + px + q = 0 » с обычным общим видом квадратного уравнения « ax 2 + bx + c = 0 », то становится видно,
что « p = b », а « q = c ».
Теперь давайте на примерах разберем, к каким уравнениям можно применять теорему Виета, а где это не целесообразно.
Так как « a = 1 » можно использовать теорему Виета.
Приведем уравнение к общему виду:
Так как « a = 3 » не следует использовать теорему Виета.
Приведем уравнение к общему виду:
Так как « a = −1 » не следует использовать теорему Виета.
Как использовать теорему Виета
Теперь мы готовы перейти к самому методу Виета для решения квадратных уравнений.
Теорема Виета для приведённых квадратных уравнений « x 2 + px + q = 0 » гласит что справедливо следующее:
| x1 + x2 = −p |
| x1 · x2 = q |
, где « x1 » и « x2 » — корни этого уравнения.
Чтобы было проще запомнить формулу Виета, следует запомнить:
«Коэффициент « p » — значит плохой, поэтому он берется со знаком минус ».
Так как в этом уравнении « a = 1 », квадратное уравнение считается приведённым, значит, можно использовать метод Виета. Выпишем коэффициенты « p » и « q ».
- p = 4
- q = −5
Запишем теорему Виета для квадратного уравнения.
| x1 + x2 = − 4 |
| x1 · x2 = −5 |
Методом подбора мы приходим к тому, что корни уравнения « x1 = −5 » и « x2 = 1 ». Запишем ответ.
Рассмотрим другой пример.
Старший коэффициент « a = 1 » поэтому можно применять теорему Виета.
| x1 + x2 = − 1 |
| x1 · x2 = −6 |
Методом подбора получим, что корни уравнения « x1 = −3 » и « x2 = 2 ». Запишем ответ.
Если у вас не получается решить уравнение с помощью теоремы Виета, не отчаивайтесь. Вы всегда можете решить любое квадратное уравнение, используя формулу для нахождения корней.
Деление уравнение на первый коэффициент
Рассмотрим уравнение, которое по заданию требуется решить, используя теорему Виета.
Сейчас в уравнении « a = 2 », поэтому перед тем, как использовать теорему Виета нужно сделать так, чтобы « a = 1 ».
Для этого достаточно разделить все уравнение на « 2 ». Таким образом, мы сделаем квадратное уравнение приведённым.
Теперь « a = 1 » и можно смело записывать формулу Виета и находить корни методом подбора.
| x1 + x2 = − (−8) |
| x1 · x2 = −9 |
| x1 + x2 = 8 |
| x1 · x2 = −9 |
Методом подбора получим, что корни уравнения « x1 = 9 » и « x2 = −1 ». Запишем ответ.
Бывают задачи, где требуется найти не только корни уравнения, но и коэффициенты самого уравнения. Например, как в такой задаче.
Корни « x1 » и « x2 » квадратного уравнения « x 2 + px + 3 = 0 » удовлетворяют условию « x2 = 3x1 ». Найти « p », « x1 », « x2 ».
Запишем теорему Виета для этого уравнения.
x 2 + px + 3 = 0
| x1 + x2 = −p |
| x1 · x2 = 3 |
По условию дано, что « x2 = 3x1 ». Подставим это выражение в систему вместо « x2».
| x1 + 3x1 = −p |
| x1 · 3x1 = 3 |
| 4x1 = −p |
| 3x1 2 = 3 |(:3) |
| 4x1 + p = 0 |
| x1 2 = 1 |
| p = −4x1 |
| x1 2 = 1 |
Решим полученное квадратное уравнение « x1 2 = 1 » методом подбора и найдем « x1 ».
x1 2 = 1
- (Первый корень) x1 = 1
- (Второй корень) x1 = −1
Мы получили два значения « x1 ». Для каждого из полученных значений найдем « p » и запишем все полученные результаты в ответ.
Теорема Виета в общем виде
В школьном курсе математики теорему Виета используют только для приведённых уравнений, где старший коэффициент « a = 1 », но, на самом деле, теорему Виета можно применить к любому квадратному уравнению.
В общем виде теорема Виета для квадратного уравнения выглядит так:
Убедимся в правильности этой теоремы на примере. Рассмотрим неприведённое квадратное уравнение.
Используем для него теорему Виета в общем виде.
Методом подбора получим, что корни уравнения « x1 = −3 » и « x2 = 2 ». Запишем ответ.
В заданиях школьной математики мы не рекомендуем использовать теорему Виета в общем виде.
Другими словами, реальную пользу теорема Виета приносит только для приведённых квадратных уравнений, в которых « a = 1 ». Именно в таких случаях она не усложняет жизнь, а позволят без дополнительных расчетов быстро найти корни.
Теорема Виета
В математике существуют специальные приемы, с которыми многие квадратные уравнения решаются очень быстро и без всяких дискриминантов. Более того, при надлежащей тренировке многие начинают решать квадратные уравнения устно, буквально «с первого взгляда».
К сожалению, в современном курсе школьной математики подобные технологии почти не изучаются. А знать надо! И сегодня мы рассмотрим один из таких приемов — теорему Виета. Для начала введем новое определение.
Квадратное уравнение вида x 2 + bx + c = 0 называется . Обратите внимание: коэффициент при x 2 равен 1. Никаких других ограничений на коэффициенты не накладывается.
- x 2 + 7 x + 12 = 0 — это приведенное квадратное уравнение;
- x 2 − 5 x + 6 = 0 — тоже приведенное;
- 2 x 2 − 6 x + 8 = 0 — а вот это нифига не приведенное, поскольку коэффициент при x 2 равен 2.
Разумеется, любое квадратное уравнение вида ax 2 + bx + c = 0 можно сделать приведенным — достаточно разделить все коэффициенты на число a . Мы всегда можем так поступить, поскольку из определения квадратного уравнения следует, что a ≠ 0.
Правда, далеко не всегда эти преобразования будут полезны для отыскания корней. Чуть ниже мы убедимся, что делать это надо лишь тогда, когда в итоговом приведенном квадратом уравнении все коэффициенты будут целочисленными. А пока рассмотрим простейшие примеры:
Задача. Преобразовать квадратное уравнение в приведенное:
- 3 x 2 − 12 x + 18 = 0;
- −4 x 2 + 32 x + 16 = 0;
- 1,5 x 2 + 7,5 x + 3 = 0;
- 2 x 2 + 7 x − 11 = 0.
Разделим каждое уравнение на коэффициент при переменной x 2 . Получим:
- 3 x 2 − 12 x + 18 = 0 ⇒ x 2 − 4 x + 6 = 0 — разделили все на 3;
- −4 x 2 + 32 x + 16 = 0 ⇒ x 2 − 8 x − 4 = 0 — разделили на −4;
- 1,5 x 2 + 7,5 x + 3 = 0 ⇒ x 2 + 5 x + 2 = 0 — разделили на 1,5, все коэффициенты стали целочисленными;
- 2 x 2 + 7 x − 11 = 0 ⇒ x 2 + 3,5 x − 5,5 = 0 — разделили на 2. При этом возникли дробные коэффициенты.
Как видите, приведенные квадратные уравнения могут иметь целые коэффициенты даже в том случае, когда исходное уравнение содержало дроби.
Теперь сформулируем основную теорему, для которой, собственно, и вводилось понятие приведенного квадратного уравнения:
. Рассмотрим приведенное квадратное уравнение вида x 2 + bx + c = 0. Предположим, что это уравнение имеет действительные корни x 1 и x 2. В этом случае верны следующие утверждения:
- x 1 + x 2 = − b . Другими словами, сумма корней приведенного квадратного уравнения равна коэффициенту при переменной x , взятому с противоположным знаком;
- x 1 · x 2 = c . Произведение корней квадратного уравнения равно свободному коэффициенту.
Примеры. Для простоты будем рассматривать только приведенные квадратные уравнения, не требующие дополнительных преобразований:
- x 2 − 9 x + 20 = 0 ⇒ x 1 + x 2 = − (−9) = 9; x 1 · x 2 = 20; корни: x 1 = 4; x 2 = 5;
- x 2 + 2 x − 15 = 0 ⇒ x 1 + x 2 = −2; x 1 · x 2 = −15; корни: x 1 = 3; x 2 = −5;
- x 2 + 5 x + 4 = 0 ⇒ x 1 + x 2 = −5; x 1 · x 2 = 4; корни: x 1 = −1; x 2 = −4.
Теорема Виета дает нам дополнительную информацию о корнях квадратного уравнения. На первый взгляд это может показаться сложным, но даже при минимальной тренировке вы научитесь «видеть» корни и буквально угадывать их за считанные секунды.
Задача. Решите квадратное уравнение:
- x 2 − 9 x + 14 = 0;
- x 2 − 12 x + 27 = 0;
- 3 x 2 + 33 x + 30 = 0;
- −7 x 2 + 77 x − 210 = 0.
Попробуем выписать коэффициенты по теореме Виета и «угадать» корни:
- x 2 − 9 x + 14 = 0 — это приведенное квадратное уравнение.
По теореме Виета имеем: x 1 + x 2 = −(−9) = 9; x 1 · x 2 = 14. Несложно заметить, что корни — числа 2 и 7; - x 2 − 12 x + 27 = 0 — тоже приведенное.
По теореме Виета: x 1 + x 2 = −(−12) = 12; x 1 · x 2 = 27. Отсюда корни: 3 и 9; - 3 x 2 + 33 x + 30 = 0 — это уравнение не является приведенным. Но мы это сейчас исправим, разделив обе стороны уравнения на коэффициент a = 3. Получим: x 2 + 11 x + 10 = 0.
Решаем по теореме Виета: x 1 + x 2 = −11; x 1 · x 2 = 10 ⇒ корни: −10 и −1; - −7 x 2 + 77 x − 210 = 0 — снова коэффициент при x 2 не равен 1, т.е. уравнение не приведенное. Делим все на число a = −7. Получим: x 2 − 11 x + 30 = 0.
По теореме Виета: x 1 + x 2 = −(−11) = 11; x 1 · x 2 = 30; из этих уравнений легко угадать корни: 5 и 6.
Из приведенных рассуждений видно, как теорема Виета упрощает решение квадратных уравнений. Никаких сложных вычислений, никаких арифметических корней и дробей. И даже дискриминант (см. урок «Решение квадратных уравнений») нам не потребовался.
Разумеется, во всех размышлениях мы исходили из двух важных предположений, которые, вообще говоря, не всегда выполняются в реальных задачах:
- Квадратное уравнение является приведенным, т.е. коэффициент при x 2 равен 1;
- Уравнение имеет два различных корня. С точки зрения алгебры, в этом случае дискриминант D > 0 — по сути, мы изначально предполагаем, что это неравенство верно.
Однако в типичных математических задачах эти условия выполняются. Если же в результате вычислений получилось «плохое» квадратное уравнение (коэффициент при x 2 отличен от 1), это легко исправить — взгляните на примеры в самом начале урока. Про корни вообще молчу: что это за задача, в которой нет ответа? Конечно, корни будут.
Таким образом, общая схема решения квадратных уравнений по теореме Виета выглядит следующим образом:
- Свести квадратное уравнение к приведенному, если это еще не сделано в условии задачи;
- Если коэффициенты в приведенном квадратном уравнении получились дробными, решаем через дискриминант. Можно даже вернуться к исходному уравнению, чтобы работать с более «удобными» числами;
- В случае с целочисленными коэффициентами решаем уравнение по теореме Виета;
- Если в течение нескольких секунд не получилось угадать корни, забиваем на теорему Виета и решаем через дискриминант.
Задача. Решите уравнение: 5 x 2 − 35 x + 50 = 0.
Итак, перед нами уравнение, которое не является приведенным, т.к. коэффициент a = 5. Разделим все на 5, получим: x 2 − 7 x + 10 = 0.
Все коэффициенты квадратного уравнения целочисленные — попробуем решить по теореме Виета. Имеем: x 1 + x 2 = −(−7) = 7; x 1 · x 2 = 10. В данном случае корни угадываются легко — это 2 и 5. Считать через дискриминант не надо.
Задача. Решите уравнение: −5 x 2 + 8 x − 2,4 = 0.
Смотрим: −5 x 2 + 8 x − 2,4 = 0 — это уравнение не является приведенным, разделим обе стороны на коэффициент a = −5. Получим: x 2 − 1,6 x + 0,48 = 0 — уравнение с дробными коэффициентами.
Лучше вернуться к исходному уравнению и считать через дискриминант: −5 x 2 + 8 x − 2,4 = 0 ⇒ D = 8 2 − 4 · (−5) · (−2,4) = 16 ⇒ . ⇒ x 1 = 1,2; x 2 = 0,4.
Задача. Решите уравнение: 2 x 2 + 10 x − 600 = 0.
Для начала разделим все на коэффициент a = 2. Получится уравнение x 2 + 5 x − 300 = 0.
Это приведенное уравнение, по теореме Виета имеем: x 1 + x 2 = −5; x 1 · x 2 = −300. Угадать корни квадратного уравнения в данном случае затруднительно — лично я серьезно «завис», когда решал эту задачу.
Придется искать корни через дискриминант: D = 5 2 − 4 · 1 · (−300) = 1225 = 35 2 . Если вы не помните корень из дискриминанта, просто отмечу, что 1225 : 25 = 49. Следовательно, 1225 = 25 · 49 = 5 2 · 7 2 = 35 2 .
Теперь, когда корень из дискриминанта известен, решить уравнение не составит труда. Получим: x 1 = 15; x 2 = −20.
Теорема Виета для квадратного уравнения

Основные понятия
Квадратное уравнение — это ax 2 + bx + c = 0, где a — первый коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Существует три вида квадратных уравнений:
- не имеют корней;
- имеют один корень;
- имеют два различных корня.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Формула для его поиска записывается так: D = b 2 − 4ac. Его свойства:
- если D 0, есть два различных корня.
В математике теоремой принято называть утверждение, у которого ранее было сформулировано доказательство.
Формула Виета
Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:
Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.
Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:
Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.
Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.
Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:
Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:
Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=”215″ src=”https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE” width=”393″>
Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=”52″ src=”https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG” width=”125″>
Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=”52″ src=”https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo” width=”112″>
Результат проделанных вычислений в том, что мы убедились в справедливости выражения:
Доказательство теоремы Виета
Дано квадратное уравнение x 2 + bx + c = 0. Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену:
Докажем, что следующие равенства верны
Чтобы найти сумму корней x₁ и x₂ подставим вместо них то, что соответствует им из правой части формул корней. Напомним, что в данном квадратном уравнении x 2 + bx + c = 0 старший коэффициент равен единице. Значит после подстановки знаменатель будет равен 2.
- Объединим числитель и знаменатель в правой части.
Раскроем скобки и приведем подобные члены:
Сократим дробь полученную дробь на 2, остается −b:
Мы доказали: x₁ + x₂ = −b.
Далее произведем аналогичные действия, чтобы доказать о равенстве x₁ * x₂ свободному члену c.
- Подставим вместо x₁ и x₂ соответствующие части из формул корней квадратного уравнения:
Перемножаем числители и знаменатели между собой:
Очевидно, в числителе содержится произведение суммы и разности двух выражений. Поэтому воспользуемся тождеством (a + b) * (a − b) = a 2 − b 2 . Получаем:
Далее произведем трансформации в числителе:
Нам известно, что D = b2 − 4ac. Подставим это выражение вместо D.
Далее раскроем скобки и приведем подобные члены:
Сократим:
Мы доказали: x₁ * x₂ = c.
Значит сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком (x₁ + x₂ = −b), а произведение корней равно свободному члену (x₁ * x₂= c). Теорема доказана.
Обратная теорема Виета
Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Она формулируется так:
Обратная теорема Виета
Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа являются корнями x 2 + bx + c = 0.
Обратные теоремы зачастую сформулированы так, что их утверждением является заключение первой теоремы. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это является утверждением.
Докажем теорему, обратную теореме Виета
Корни x₁ и x₂ обозначим как m и n. Тогда утверждение будет звучать следующим образом: если сумма чисел m и n равна второму коэффициенту x 2 + bx + c = 0, взятому с противоположным знаком, а произведение равно свободному члену, то числа m и n являются корнями x 2 + bx + c = 0.
Зафиксируем, что сумма m и n равна −b, а произведение равно c.
Чтобы доказать, что числа m и n являются корнями уравнения, нужно поочередно подставить буквы m и n вместо x, затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями x 2 + bx + c = 0.
- Выразим b из равенства m + n = −b. Это можно сделать, умножив обе части на −1:
Подставим m в уравнение вместо x, а выражение −m − n подставим вместо b:
При x = m получается верное равенство. Значит число m является искомым корнем.
- Аналогично докажем, что число n является корнем уравнения. Подставим вместо x букву n, а вместо c подставим m * n, поскольку c = m * n.
- При x = n получается верное равенство. Значит число n является искомым корнем.
Мы доказали: числа m и n являются корнями уравнения x 2 + bx + c = 0.
Примеры
Для закрепления знаний рассмотрим примеры решения уравнений по теореме, обратной теореме Виета.
Дано: x 2 − 6x + 8 = 0.
Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
2 − 6x + 8 = 0″ height=”59″ src=”https://lh6.googleusercontent.com/tFokx3SM93Hwlr7ZM9BqX1xiHKv_2dUIB9MoNa8RAwSTmQKXdCcqcFXxTZmxNGw7bOVek-RzRXqBkoCqnYMiqIYVwKhfnHeU-7mA03feEqJTlyKB7e-OsTTKgPaOlddfiaTGszcv” width=”99″>
Имея эти два равенства можно подобрать подходящие корни, которые будут удовлетворять как равенству обоим равенствам системы.
Подбор корней удобнее выполнять с помощью их произведения. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.
Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. Значения 4 и 2 подходят обоим равенствам:
Значит числа 4 и 2 являются корнями уравнения x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=”57″ src=”https://lh3.googleusercontent.com/rohB7Bvd-elMhTxEUuOhKqLJjqLAvo9VlJxZvOnMeDAHARfKT-SYOWb1WXTTWEN2h0oKbLl6wH7lc0IWL_vH3Si2AJGAGXVn8TPFDT_J1Wu2WeoQ-WP1qgXjCnZ99tWUkK2BOvF2″ width=”64″>
Неприведенное квадратное уравнение
Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым, то есть его первый коэффициент равен единице:
ax 2 + bx + c = 0, где а = 1.
Если квадратное уравнение не является приведенным, но задание связано с применением теоремы, нужно обе части разделить на коэффициент, который располагается перед x 2 .
- Получилось следующее приведенное уравнение:
- Получается коэффициент равен, свободный член —. Значит сумма и произведение корней будут иметь вид:
Рассмотрим пример неприведенного уравнения: 4x 2 + 5x + 1 = 0. Разделим обе его части на коэффициент перед x 2 , то есть на 4.
Записывайте вашего ребенка на бесплатное вводное занятие по математике в Skysmart: порешаем задачки и головоломки на интерактивной платформе и покажем, что математика может быть увлекательным путешествием!
Теорема Виета, формулы Виета
Между корнями и коэффициентами квадратного уравнения, помимо формул корней, существуют другие полезные соотношения, которые задаются теоремой Виета. В этой статье мы дадим формулировку и доказательство теоремы Виета для квадратного уравнения. Дальше рассмотрим теорему, обратную теореме Виета. После этого разберем решения наиболее характерных примеров. Наконец, запишем формулы Виета, задающие связь между действительными корнями алгебраического уравнения степени n и его коэффициентами.
Навигация по странице.
- Теорема Виета, формулировка, доказательство.
- Теорема, обратная теореме Виета.
- Примеры использования теоремы Виета.
- Формулы Виета.
Теорема Виета, формулировка, доказательство
Из формул корней квадратного уравнения a·x 2 +b·x+c=0 вида , где D=b 2 −4·a·c , вытекают соотношения x1+x2=−b/a , x1·x2=c/a . Эти результаты утверждаются теоремой Виета:
Если x1 и x2 – корни квадратного уравнения a·x 2 +b·x+c=0 , то сумма корней равна отношению коэффициентов b и a , взятому с противоположным знаком, а произведение корней равно отношению коэффициентов c и a , то есть,  .
.
Доказательство теоремы Виета проведем по следующей схеме: составим сумму и произведение корней квадратного уравнения, используя известные формулы корней, после этого преобразуем полученные выражения, и убедимся, что они равны −b/a и c/a соответственно.
Начнем с суммы корней, составляем ее . Теперь приводим дроби к общему знаменателю, имеем . В числителе полученной дроби раскрываем скобки, после чего приводим подобные слагаемые: . Наконец, после сокращения дроби на 2 , получаем . Этим доказано первое соотношение теоремы Виета для суммы корней квадратного уравнения. Переходим ко второму.
Составляем произведение корней квадратного уравнения: . Согласно правилу умножения дробей, последнее произведение можно записать как . Теперь выполняем умножение скобки на скобку в числителе, но быстрее свернуть это произведение по формуле разности квадратов, так . Дальше, вспомнив определение квадратного корня, выполняем следующий переход . А так как дискриминанту квадратного уравнения отвечает формула D=b 2 −4·a·c , то в последнюю дробь вместо D можно подставить b 2 −4·a·c , получаем . После раскрытия скобок и приведения подобных слагаемых приходим к дроби , а ее сокращение на 4·a дает . Этим доказано второе соотношение теоремы Виета для произведения корней.
Если опустить пояснения, то доказательство теоремы Виета примет лаконичный вид:
,
.
Остается лишь заметить, что при равном нулю дискриминанте квадратное уравнение имеет один корень. Однако, если считать, что уравнение в этом случае имеет два одинаковых корня, то равенства из теоремы Виета также имеют место. Действительно, при D=0 корень квадратного уравнения равен , тогда и , а так как D=0 , то есть, b 2 −4·a·c=0 , откуда b 2 =4·a·c , то .
На практике наиболее часто теорема Виета используется применительно к приведенному квадратному уравнению (со старшим коэффициентом a , равным 1 ) вида x 2 +p·x+q=0 . Иногда ее и формулируют для квадратных уравнений именно такого вида, что не ограничивает общности, так как любое квадратное уравнение можно заменить равносильным уравнением, выполнив деление его обеих частей на отличное от нуля число a . Приведем соответствующую формулировку теоремы Виета:
Сумма корней приведенного квадратного уравнения x 2 +p·x+q=0 равна коэффициенту при x , взятому с противоположным знаком, а произведение корней – свободному члену, то есть, x1+x2=−p , x1·x2=q .
Теорема, обратная теореме Виета
Вторая формулировка теоремы Виета, приведенная в предыдущем пункте, указывает, что если x1 и x2 корни приведенного квадратного уравнения x 2 +p·x+q=0 , то справедливы соотношения x1+x2=−p , x1·x2=q . С другой стороны, из записанных соотношений x1+x2=−p , x1·x2=q следует, что x1 и x2 являются корнями квадратного уравнения x 2 +p·x+q=0 . Иными словами, справедливо утверждение, обратное теореме Виета. Сформулируем его в виде теоремы, и докажем ее.
Если числа x1 и x2 таковы, что x1+x2=−p и x1·x2=q , то x1 и x2 являются корнями приведенного квадратного уравнения x 2 +p·x+q=0 .
После замены в уравнении x 2 +p·x+q=0 коэффициентов p и q их выражения через x1 и x2 , оно преобразуется в равносильное уравнение x 2 −(x1+x2)·x+x1·x2=0 .
На этом завершено доказательство теоремы, обратной теореме Виета.
Примеры использования теоремы Виета
Пришло время поговорить о практическом применении теоремы Виета и обратной ей теоремы. В этом пункте мы разберем решения нескольких наиболее характерных примеров.
Начнем с применения теоремы, обратной теореме Виета. Ее удобно применять для проверки, являются ли данные два числа корнями заданного квадратного уравнения. При этом вычисляется их сумма и разность, после чего проверяется справедливость соотношений . Если выполняются оба этих соотношения, то в силу теоремы, обратной теореме Виета, делается вывод, что данные числа являются корнями уравнения. Если же хотя бы одно из соотношений не выполняется, то данные числа не являются корнями квадратного уравнения. Такой подход можно использовать при решении квадратных уравнений для проверки найденных корней.
Какая из пар чисел 1) x1=−5 , x2=3 , или 2) , или 3) является парой корней квадратного уравнения 4·x 2 −16·x+9=0 ?
Коэффициентами заданного квадратного уравнения 4·x 2 −16·x+9=0 являются a=4 , b=−16 , c=9 . Согласно теореме Виета сумма корней квадратного уравнения должна быть равна −b/a , то есть, 16/4=4 , а произведение корней должно быть равно c/a , то есть, 9/4 .
Теперь вычислим сумму и произведение чисел в каждой из трех заданных пар, и сравним их с только что полученными значениями.
В первом случае имеем x1+x2=−5+3=−2 . Полученное значение отлично от 4 , поэтому дальнейшую проверку можно не осуществлять, а по теореме, обратной теореме Виета, сразу сделать вывод, что первая пара чисел не является парой корней заданного квадратного уравнения.
Переходим ко второму случаю. Здесь , то есть, первое условие выполнено. Проверяем второе условие: , полученное значение отлично от 9/4 . Следовательно, и вторая пара чисел не является парой корней квадратного уравнения.
Остался последний случай. Здесь и . Оба условия выполнены, поэтому эти числа x1 и x2 являются корнями заданного квадратного уравнения.
Теорему, обратную теореме Виета, на практике можно использовать для подбора корней квадратного уравнения. Обычно подбирают целые корни приведенных квадратных уравнений с целыми коэффициентами, так как в других случаях это сделать достаточно сложно. При этом пользуются тем фактом, что если сумма двух чисел равна второму коэффициенту квадратного уравнения, взятому со знаком минус, а произведение этих чисел равно свободному члену, то эти числа являются корнями данного квадратного уравнения. Разберемся с этим на примере.
Возьмем квадратное уравнение x 2 −5·x+6=0 . Чтобы числа x1 и x2 были корнями этого уравнения, должны выполняться два равенства x1+x2=5 и x1·x2=6 . Остается подобрать такие числа. В данном случае это сделать достаточно просто: такими числами являются 2 и 3 , так как 2+3=5 и 2·3=6 . Таким образом, 2 и 3 – корни данного квадратного уравнения.
Теорему, обратную теореме Виета, особенно удобно применять для нахождения второго корня приведенного квадратного уравнения, когда уже известен или очевиден один из корней. В этом случае второй корень находится из любого из соотношений .
Для примера возьмем квадратное уравнение 512·x 2 −509·x−3=0 . Здесь легко заметить, что единица является корнем уравнения, так как сумма коэффициентов этого квадратного уравнения равна нулю. Итак, x1=1 . Второй корень x2 можно найти, например, из соотношения x1·x2=c/a . Имеем 1·x2=−3/512 , откуда x2=−3/512 . Так мы определили оба корня квадратного уравнения: 1 и −3/512 .
Понятно, что подбор корней целесообразен лишь в самых простых случаях. В остальных случаях для поиска корней можно применить формулы корней квадратного уравнения через дискриминант.
Еще одно практическое применение теоремы, обратной теореме Виета, состоит в составлении квадратных уравнений по заданным корням x1 и x2 . Для этого достаточно вычислить сумму корней, которая дает коэффициент при x с противоположным знаком приведенного квадратного уравнения, и произведение корней, которое дает свободный член.
Напишите квадратное уравнение, корнями которого являются числа −11 и 23 .
Обозначим x1=−11 и x2=23 . Вычисляем сумму и произведение данных чисел: x1+x2=12 и x1·x2=−253 . Следовательно, указанные числа являются корнями приведенного квадратного уравнения со вторым коэффициентом −12 и свободным членом −253 . То есть, x 2 −12·x−253=0 – искомое уравнение.
Теорема Виета очень часто используется при решении заданий, связанных со знаками корней квадратных уравнений. Как же связана теорема Виета со знаками корней приведенного квадратного уравнения x 2 +p·x+q=0 ? Приведем два соответствующих утверждения:
- Если свободный член q – положительное число и если квадратное уравнение имеет действительные корни, то либо они оба положительные, либо оба отрицательные.
- Если же свободный член q – отрицательное число и если квадратное уравнение имеет действительные корни, то их знаки различны, другими словами, один корень положительный, а другой – отрицательный.
Эти утверждения вытекают из формулы x1·x2=q , а также правил умножения положительных, отрицательных чисел и чисел с разными знаками. Рассмотрим примеры их применения.
Положительны ли оба корня квадратного уравнения x 2 −64·x−21=0 ?
Если данное квадратное уравнение имеет два корня, то они не могут быть оба положительными, так как по теореме Виета для них должно выполняться равенство x1·x2=−21 , которое невозможно при положительных x1 и x2 .
При каких значениях параметра r квадратное уравнение x 2 +(r+2)·x+r−1=0 имеет два действительных корня, имеющих разные знаки.
Сначала определим, при каких r это уравнение имеет два корня. Для этого найдем дискриминант, и выясним, при каких r он положителен. По формуле дискриминанта находим D=(r+2) 2 −4·1·(r−1)= r 2 +4·r+4−4·r+4=r 2 +8 , значение выражения r 2 +8 положительно при любых действительных r , таким образом, D>0 при любых действительных r . Следовательно, исходное квадратное уравнение имеет два корня при любых действительных значениях параметра r .
Теперь выясним, когда корни имеют разные знаки. Если знаки корней различны, то их произведение отрицательно, а по теореме Виета произведение корней приведенного квадратного уравнения равно свободному члену. Следовательно, нас интересуют те значения r , при которых свободный член r−1 отрицателен. Таким образом, чтобы найти интересующие нас значения r , надо решить линейное неравенство r−1 , откуда находим r .
Формулы Виета
Выше мы говорили о теореме Виета для квадратного уравнения и разбирали утверждаемые ей соотношения. Но существуют формулы, связывающие действительные корни и коэффициенты не только квадратных уравнений, но и кубических уравнений, уравнений четверной степени, и вообще, алгебраических уравнений степени n . Их называют формулами Виета.
Запишем формулы Виета для алгебраического уравнения степени n вида , при этом будем считать, что оно имеет n действительных корней x1, x2, …, xn (среди них могут быть совпадающие):

Получить формулы Виета позволяет теорема о разложении многочлена на линейные множители, а также определение равных многочленов через равенство всех их соответствующих коэффициентов. Так многочлен и его разложение на линейные множители вида равны. Раскрыв скобки в последнем произведении и приравняв соответствующие коэффициенты, получим формулы Виета.
В частности при n=2 имеем уже знакомые нам формулы Виета для квадратного уравнения .
Для кубического уравнения формулы Виета имеют вид

Остается лишь заметить, что в левой части формул Виета находятся так называемые элементарные симметрические многочлены.